Salve a tutti. Premetto che tutto quanto segue, non ha alcun tipo di pretesa, ma ha il solo scopo di illustrare ciò che si può provare fare con qualche strumento di misura. Da qualche tempo, anche se non in modo intensivo, seguo il vostro bel sito. Non nascondo che leggere le vostre recensioni intorno agli apparecchi Grundig ha scatenato in me, una vera curiosità. Curiosità che ho appagato quasi immediatamente, riesumando un vecchio Grundig R20 appartenuto a mio padre. L’apparecchio, anche se ben imballato, giaceva in un ripostiglio da più di 25 anni. Non ostante il lungo tempo che ha trascorso inutilizzato il ricevitore, una volta tolto dall’imballo, appare in perfette condizioni estetiche e mostra un look ancora accattivante, non ostante i 40 anni passati dalla sua costruzione. Ecco il ricevitore come appare una volta fuori dall’imballo.

sintoamplificatore Grundig R20
Fig. 1 – Il sintoamplificatore Grundig R20
Dopo così tanto tempo dall’ultimo utilizzo, mi aspettavo il peggio e, invece, all’accensione le cose sembrano andare bene. A questo punto, la curiosità aumenta. Apro nuovamente il ripostiglio ed estraggo dal loro imballo, 2 casse Grundig 850 con tutti i cavi di collegamento. Casse che erano originariamente a corredo del sintoamplificatore R20. Organizzo velocemente un po’ di posto, collego le casse, riaccendo e qui, ora, c’è un’eccezione rappresentata da un po’ di disturbi dovuti alla propagazione del transiente iniziale. Forse c’è qualche problema di filtraggio. Del resto, in apparecchi così vecchiotti il fatto che non tutto sia ok è normale. Ciò non ostante, provo a sintonizzare e ascoltare una stazione radio FM tra le mie preferite. La sorpresa è grande davvero! Sto ascoltando una sonorità decisamente buona, almeno per le mie orecchie, soprattutto in considerazione del fatto che la sorgente è captata con un cavo bifilare posticcio a simulazione di un dipolo; situazione che non è certamente il meglio possibile. Tuttavia, il suono è caldo e accogliente e se non fossi certo che proviene da un sistema a transistori, direi che si ascolta qualcosa di abbastanza vicino a un suono valvolare, forse per effetto del filtro contour inserito, forse per il buon contributo delle casse, forse per la buona topologia dello schema elettrico, non saprei dire. Ad ogni modo trovandomi a disporre, per motivi che esulano dal settore audio, di un laboratorio abbastanza attrezzato; decido di mettere il ricevitore R20 sul banco di prova, per vedere cosa salta fuori dopo quasi 40 anni. Proverò a fare un po’ di misure sul sintoampli, secondo quelle che furono le specifiche e le norme utilizzate dal costruttore, cioè le Din 45-500.
Gli Strumenti di misura
Gli strumenti a mia disposizione che utilizzerò, di volta in volta, sono i seguenti:
- Oscilloscopi Analogici: Philips/Fluke PM 3055 60MHz BP e Grundig MO53 50MHz BP
- Oscilloscopio Digitale: Chauvin-Arnoux CA 912 20MHz BP
- Millivoltmetro: true RMS Marconi 2610 controllato in temperatura.
- Multimetro Digitale: true RMS Schlumberber Solartron 7150 Plus
- Frequenzimetro: Racal Dana universal counter 9902 – 50MHz autoranging.
- Distorsiometro Automatico: GW Gad 201B autoranging.
- Generatori di Funzione: Kikusui Model 459 banda 0.01Hz ÷ 1MHz Low Distortion / Phlips PM 5133s banda 0.01Hz ÷ 2MHz Low Distortion e Philips PM 5190 LF Sintetizzatore quarzato di forme d’onda banda 0.001Hz ÷ 2MHz.
- Dummy Load da 150Watt auto-costruito in sostituzione delle casse.
Qui di seguito le immagini del banco di misura figura 2 e degli strumenti utilizzati fig. 3,4,5 e 6.

Fig. 2 – Il banco Strumenti
Fig. 2 – Il banco Strumenti

millivoltmetro termo-controllato Marconi 2610, l’oscilloscopio analogico Philips PM 3025 e l’oscilloscopio analogico Grundig MO53
Fig. 3 – Dall’alto in basso, millivoltmetro termo-controllato Marconi 2610, l’oscilloscopio analogico Philips PM 3025 e l’oscilloscopio analogico Grundig MO53

Fig. 4 – Dall’alto in basso, multimetro Schlumberger Solartron 7150Plus, frequenzimetro
Fig. 4 – Dall’alto in basso, multimetro Schlumberger Solartron 7150Plus, frequenzimetro
Racal-Dana 9902 e distorsiometro automatico GW GAD-201B

Fig. 5 – Dall’alto in basso, Sintetizzatore quarzato di forme d’onda Philips 5190 LF Low Distortion, Generatore Philips PM 5133S Low Distortion e oscilloscopio digitale Chauvin-Arnoux CA 912
Fig. 5 – Dall’alto in basso, Sintetizzatore quarzato di forme d’onda Philips 5190 LF Low Distortion, Generatore Philips PM 5133S Low Distortion e oscilloscopio digitale Chauvin-Arnoux CA 912

Fig. 6 – Il dummy load auto-costruito (non anti-induttivo) da 150 Watt, termostatato e raffreddato a circolazione d’aria forzata.
Fig. 6 – Il dummy load auto-costruito (non anti-induttivo) da 150 Watt, termostatato e raffreddato a circolazione d’aria forzata.
Per le informazioni tecniche su misure audio ho sempre fatto riferimento, durante le sessioni di misura, alle raccomandazioni contenute nei seguenti testi e/o siti:
- Bob Metzler – Audio Measurement Handbook – ed. Audio Precision.
- Robert A. Pease – The right equipment is essential for effective troubleshooting – ed. National Semiconductor Corporation.
- Alta Fedeltà – Concezione, misure, realizzazione – ed. ETI.
- RMS Voltmeter – ed. Hewlett-Packard.
- Clement Brown – Audio & HiFi – ed. Jackson.
- Amplificatori di bassa frequenza e HiFi – ed. Philips/Elcoma.
- M. Martini & G. Zanarini – Misure elettroniche e radio elettroniche – ed. Zanichelli.
- Acoustic Handbook – Application Note 100 ed. Hewlett-Packard.
- Gordon J. King – The Audio Handbook – ed. Newnes-Butterworths.
- Bruel & Kjaer – Application Notes
Sfortunatamente, come avrete capito, posso solo fare analisi nel dominio del tempo e non anche in quello della frequenza, poiché tra i vari strumenti a mia disposizione manca l’analizzatore di spettro. Tutto ciò significa che per la determinazione della THD, dovrò forzatamente affidarmi a un distorsiometro.
Considerazioni iniziali
Qualche considerazione del tutto generale va assolutamente fatta, prima di affrontare le misure che proverò ad attuare. Di qui in avanti chiamerò, per semplicità espositiva, il Receiver R20 con il sostitutivo “DST” = dispositivo sotto test. Uno schema del tutto generale di riferimento per le misure che farò potrebbe essere, semplificando molto, quello di figura 7.
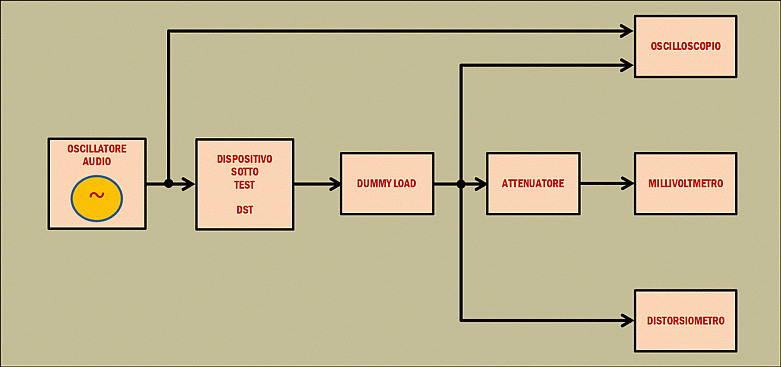
Fig. 7 – Disposizione strumentale di misura semplificata.
Fig. 7 – Disposizione strumentale di misura semplificata.
La Caratteristica ingresso/uscita del carico fittizio
Poiché, per tutte le misure, utilizzerò il carico fittizio da 150Watt in sostituzione delle casse, inizierò proprio da questo strumento. In particolare, controllerò il suo comportamento di fase al crescere della frequenza. Faccio questo per essere certo che le resistenze del carico fittizio su cui andranno a scaricarsi i finali, rappresentino quanto maggiormente possibile una pura resistenza, almeno nel range audio. Le misure, tuttavia, si estenderanno fino alla soglia dei 100KHz. Le frequenze di controllo sono state selezionate come segue: 200Hz, 1KHz, 20KHz, 50KHz e 100KHz.
Lo schema di controllo è il seguente:
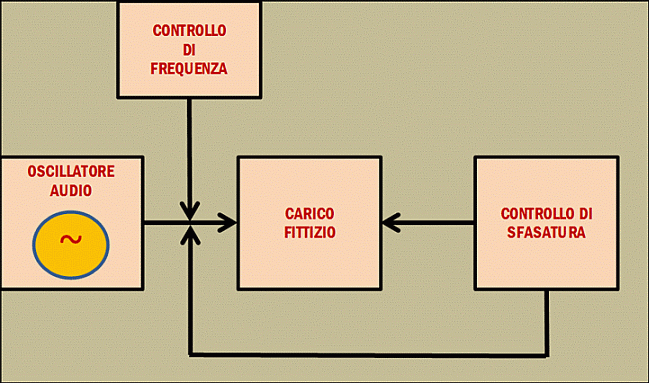
Fig. 8 – Controllo eventuale sfasatura sul carico fittizio.
Fig. 8 – Controllo eventuale sfasatura sul carico fittizio.
Originariamente il carico fittizio auto-costruito, non è stato concepito per lavorare in frequenza avendo utilizzato resistenze a filo corazzate. E’ ben noto, infatti, come tali resistenze siano costruite avvolgendo un filo metallico su un supporto cilindrico, generalmente costituito da ceramica. Il costruttore (ARCOL) dichiara per tali resistori le seguenti specifiche:
ARCOL Resistors Characteristics
Tolerance (Code): Standard ±5% (J) and ±10% (K). Also available ±1% (F), ±2% (G) and ±3% (H)
Tolerance for low Ω values: Typically ≥ R05 ±5% ≤ R047 ±10%
Temperature coefficients: Typical values < 1K 100ppm Std. > 1K 25ppm Std.
Insulation resistance (Dry): 10,000 MΩ minimum
Power dissipation: At high ambient temperature dissipation derates linearly to zero at 200°C
Ohmic values: From R005 to 100K depending on wattage size
Low inductive (NHS): Specify by adding N before HS Series code, e.g. NHS50
Per di più, le resistenze a filo corazzate non appartengono alla serie NHS, cioè low inductive quindi, è assolutamente ragionevole verificare il loro comportamento in frequenza. Come ben risaputo, ogni avvolgimento rende nota la sua esistenza al variare della frequenza. Pertanto, eseguirò una serie di misure pilotando il carico fittizio a diverse frequenze con un segnale sinusoidale e contemporaneamente controllerò, con l’oscilloscopio, l’eventuale presenza di sfasamento tra l’ingresso e l’uscita del carico fittizio stesso. Ho eseguito le misure sia in modalità normale, sia in modalità X-Y. Come ho già detto, lo scopo non è quello di misurare un angolo di fase quando si presenti, ma è soltanto quello di osservare a quale frequenza le resistenze a filo iniziano a mostrare reattanza di autoinduzione. Tutto ciò per essere certo che tali effetti non si presentino nel range in cui farò le misurazioni sul DST, cioè essenzialmente da 20Hz a 20KHz. Forse avrei potuto fare a meno di questo controllo, se le resistenze impiegate fossero state del tipo anti induttivo (avvolgimento Ayrton-Perry), perché la loro reattanza sarebbe stata resa trascurabile, almeno in Bassa frequenza, dal costruttore stesso. Anche se la questione resistenze antinduttive è ancora aperta e controversa, in campo audio. Generalmente gli accorgimenti tipo Ayrton-Perry sono tutti basati sul principio di far percorrere alla corrente, in verso opposto, le spire contigue dell’avvolgimento così da rendere l’induttanza complessiva mediamente nulla. Nelle immagini che seguono, dalla figura 12 fino alla figura 21, nella rappresentazione X-Y, la traccia non è posizionata esattamente in centro schermo come si fa per ottenere misure di angolo di fase, in quanto, sto solo cercando a quale frequenza iniziano a mostrarsi effetti indesiderati. In questo caso particolare di segnali con ugual frequenza, e relativamente alle figure 13, 15, 17, 19, 21 in modalità X-Y, mi aspetto che si presentino alcuni dei seguenti casi:
- Segnali in fase: sull’oscilloscopio si vede una retta nel primo e terzo quadrante.
- Segnali in opposizione fase: sull’oscilloscopio si vede una retta nel secondo e quarto quadrante.
- Segnali in fase e con la stessa ampiezza: sull’oscilloscopio si vede una retta inclinata di 45°.
- Segnali in opposizione di fase e con la stessa ampiezza: sull’oscilloscopio si vede una retta inclinata di 135°.
- Segnali in quadratura: in questo caso sull’oscilloscopio si vede un’ellisse con eccentricità più o meno schiacciata, a seconda dei valori relativi delle ampiezze presenti sull’asse X o sull’asse Y.
- Segnali in quadratura e con la stessa ampiezza: in questo caso sull’oscilloscopio si vede un cerchio.
Riferimento generale per l’interpretazione della modalità X-Y riferita a due sinusoidi, sono le figure di Lissajous presentate di seguito dove con φ si intende l’angolo di fase, figure 9 e 10.
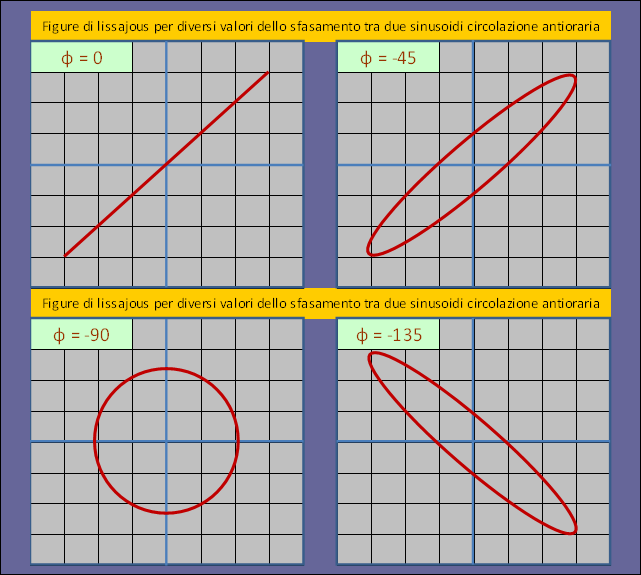
Fig. 9 – Figure base di Lissajous
Fig. 9 – Figure base di Lissajous
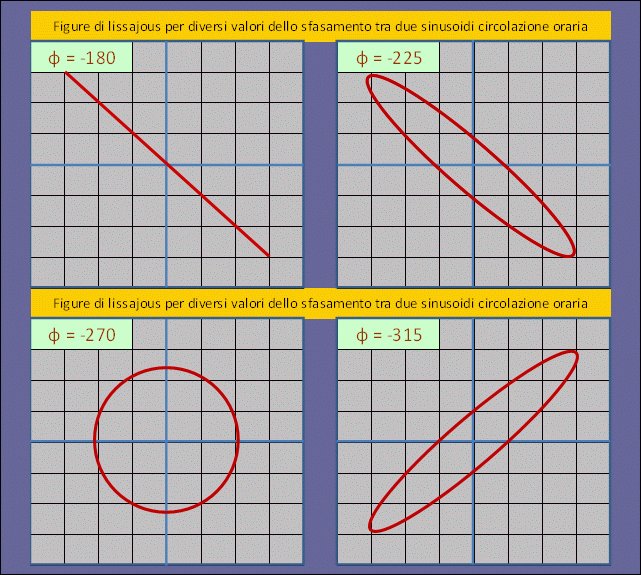
Fig. 10 – Figure base di Lissajous
Fig. 10 – Figure base di Lissajous
Le figure che mostrano i risultati di tale analisi sul carico fittizio, dalla 12 alla 21, vanno lette a gruppi abbinati. Infatti, per ogni frequenza immessa, 20Hz, 100Hz, 1KHz, 20KHz, 50KHz e 100KHz, è sempre presente anche un’immagine in modalità normale. Nell’immagine in modalità normale, è possibile apprezzare, tra le due curve, (quella superiore = segnale in ingresso e quella inferiore = segnale in uscita), dove si mostri sfasatura.
Osservando le immagini, si vede bene come ciò che avviene tra ingresso e uscita nel carico fittizio, non mostri sfasatura apprezzabile nel range 20Hz ÷ 20KHz, figure dalla 12 alla 18.
Una situazione diversa si mostra partendo da 50kHz in su – Fig. 19 – e da quel punto in poi, man mano che si aumenta la frequenza del segnale sinusoidale. L’inizio di quadratura appare chiara già a 50kHz e diviene ancor più evidente a 100kHz, figure 20 e 21. Chiaro segno che oltre i 50kHz il fenomeno di autoinduttanza si mostra in modo evidente. Con quanto evidenziato fino a questo punto posso affermare che il contributo dell’autoinduttanza, tra ingresso e uscita nel carico fittizio, è tale da non produrre effetti indesiderati in banda audio 20Hz ÷ 20kHz.
Nella figura 21, si vede la rappresentazione X-Y della caratteristica ingresso/uscita del carico fittizio, pilotato con segnale sinusoidale alla frequenza di 100kHz. Prima di scattare l’immagine, ho badato a ridurre l’intensità del fascio e in seguito, ho messo a ground (comando GND) i due canali X-Y dell’oscilloscopio. Facendo questo, ho potuto portare esattamente al centro dello schermo il pennello elettronico, in modo di poter ottenere in AC la figura ellisse di sfasatura perfettamente centrata. Questa manovra permette, se lo si vuole, di leggere esattamente le dimensioni dell’ellisse di sfasatura secondo quanto illustrato in figura 11 e calcolare, il valore dell’angolo di sfasatura.
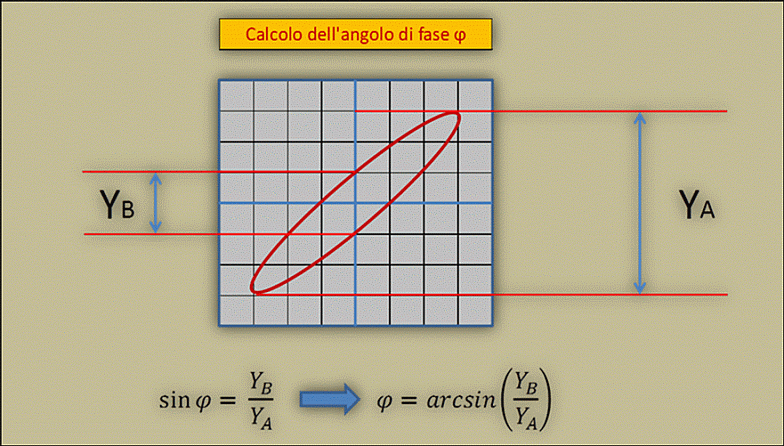
Fig. 11 – Calcolo dell’angolo di fase con segnali sinusoidali isofrequenziali
Fig. 11 – Calcolo dell’angolo di fase con segnali sinusoidali isofrequenziali
Vediamo qui di seguito tutte le immagini concernenti, le varie frequenze iniettate nel carico fittizio e la sua risposta al segnale applicato in ingresso.
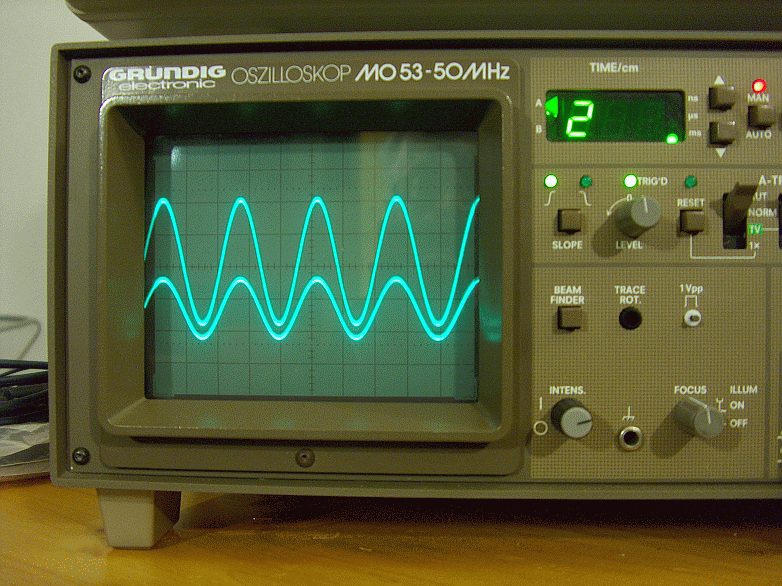
Fig. 12 – Fase ingresso uscita sul carico fittizio a 200Hz modalità normale
Fig. 12 – Fase ingresso uscita sul carico fittizio a 200Hz modalità normale
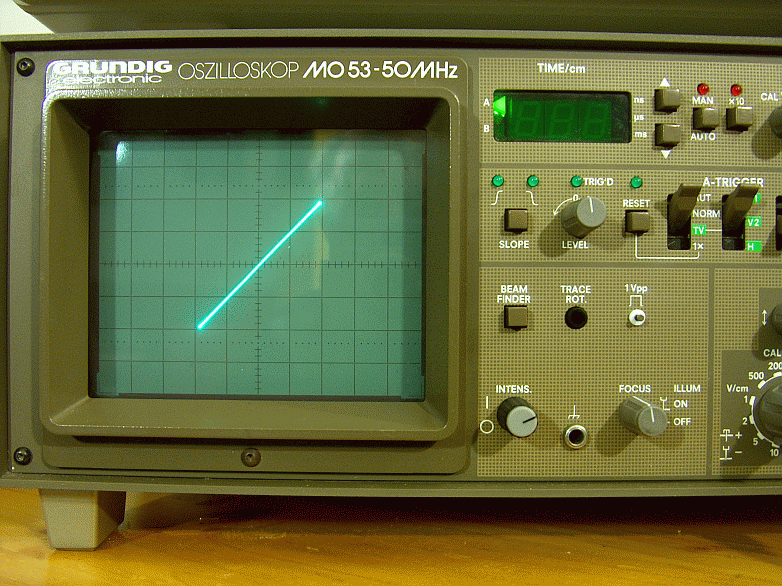
Fig. 13 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 200Hz
Fig. 13 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 200Hz
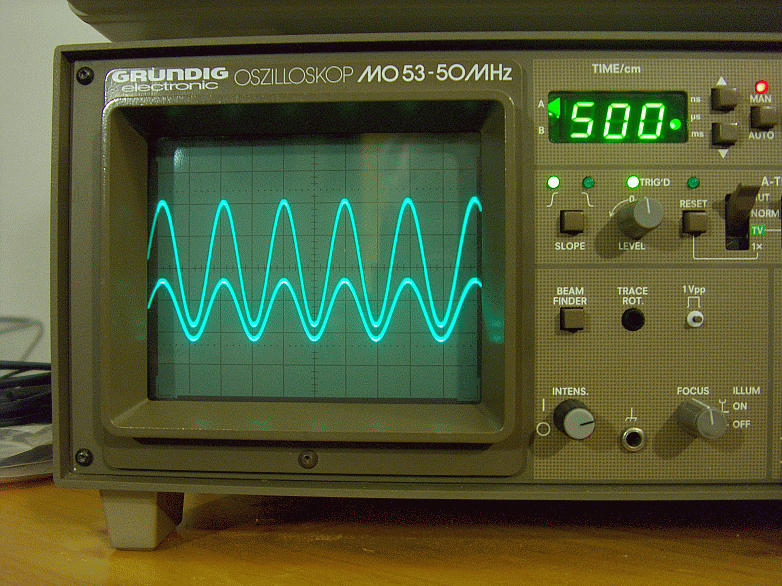
Fig. 14 – Fase ingresso uscita sul carico fittizio a 1000Hz modalità normale
Fig. 14 – Fase ingresso uscita sul carico fittizio a 1000Hz modalità normale
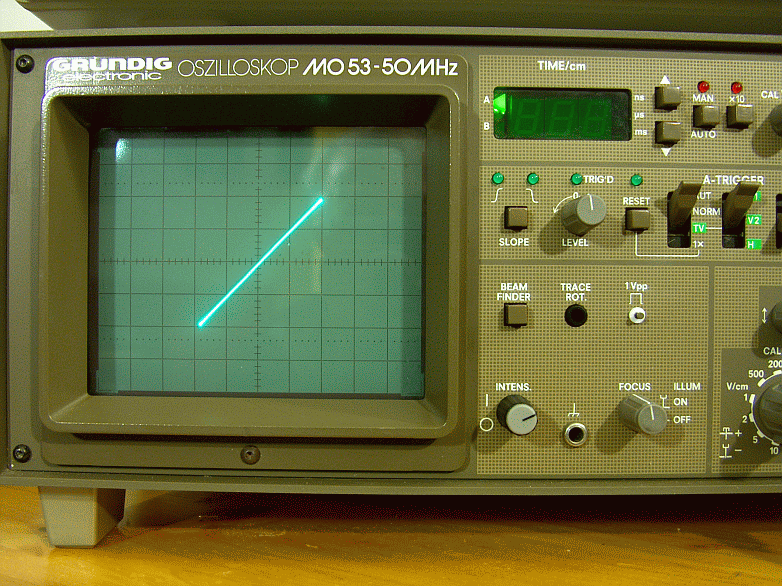
Fig. 15 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 1000Hz
Fig. 15 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 1000Hz
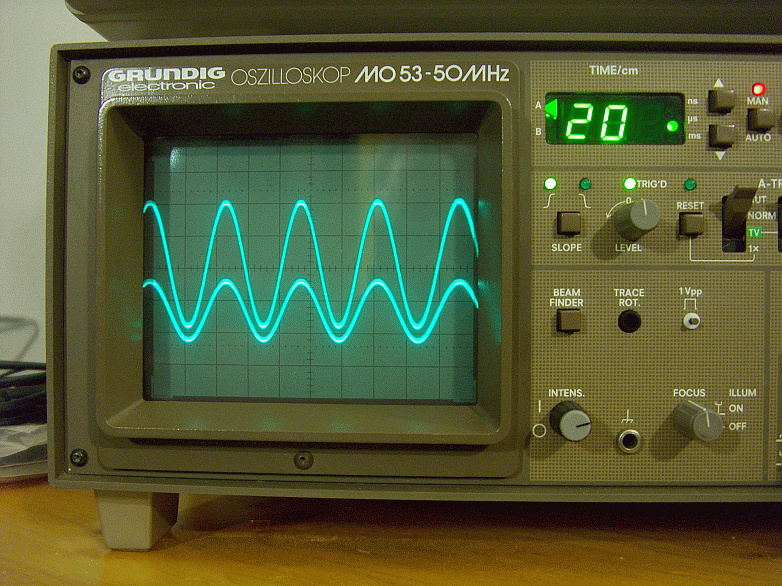
Fig. 16 – Fase ingresso uscita sul carico fittizio a 20000Hz modalità normale
Fig. 16 – Fase ingresso uscita sul carico fittizio a 20000Hz modalità normale
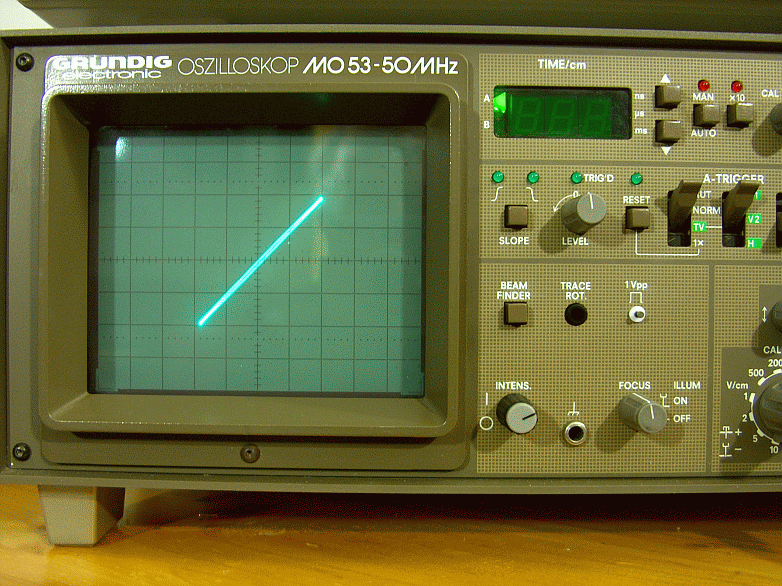
Fig. 17 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 20000Hz
Fig. 17 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 20000Hz
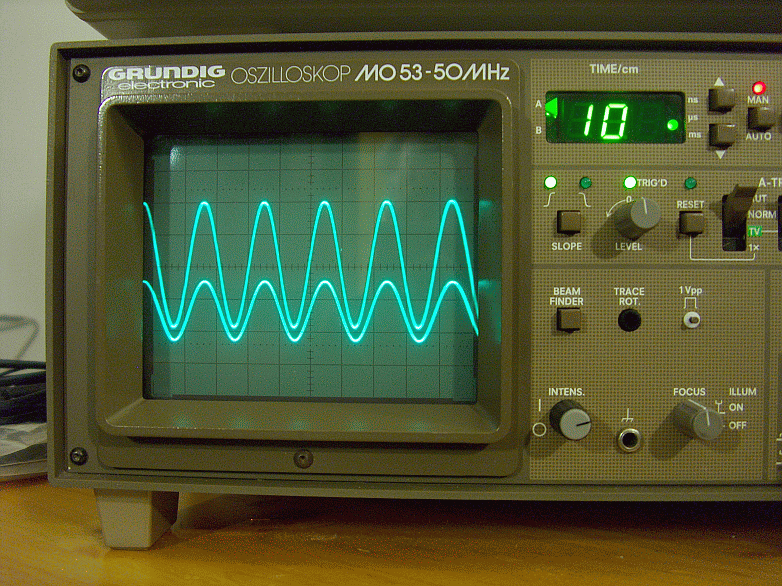
Fig. 18 – Fase ingresso uscita sul carico fittizio a 50000Hz modalità normale
Fig. 18 – Fase ingresso uscita sul carico fittizio a 50000Hz modalità normale
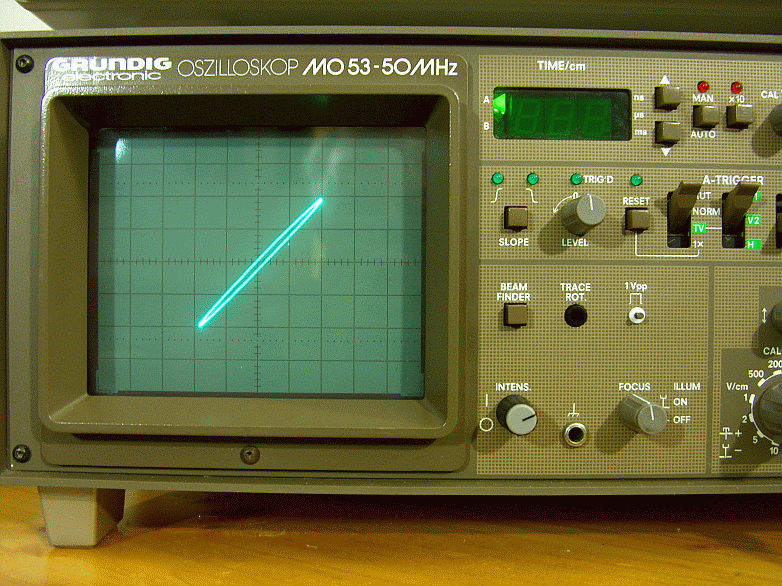
Fig. 19 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 50000Hz
Fig. 19 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 50000Hz
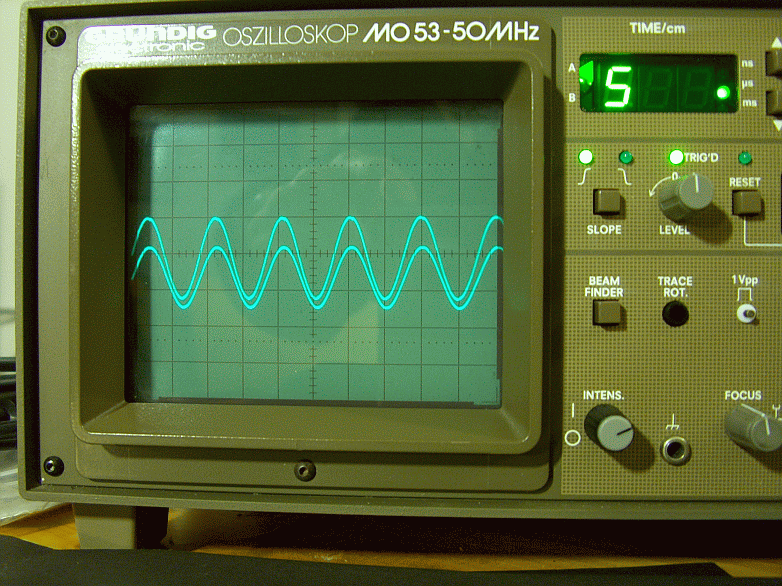
Fig. 20 – Fase ingresso uscita sul carico fittizio a 100000Hz modalità normale
Fig. 20 – Fase ingresso uscita sul carico fittizio a 100000Hz modalità normale

Fig. 21 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 100000Hz
Fig. 21 – Fase ingresso uscita in modalità X,Y sul carico fittizio a 100000Hz
Naturalmente, ho già messo in cantiere la realizzazione di un nuovo carico fittizio 4 – 8 ohm adeguato in potenza, che sarà equipaggiato con resistenze corazzate antinduttive. Questo perché, in quello stesso ripostiglio da cui ho estratto il DST, si trovano pure: un Grundig R48, un Philips 22RH521 e un Philips 22RH550 più una radio sempre Philips 22RH651. Tutti apparecchi che, prima o poi, vorrei sottoporre a qualche misura.
Inoltre, aver speso qualche parola sull’angolo di sfasatura tra due segnali sinusoidali e su come tale angolo possa essere misurato, tornerà utile quando dovrò capire quale sia la vera posizione di flat dei controlli di tono. Ora, avendo potuto osservare che nel range audio 20Hz ÷20kHz, il carico fittizio non crea vistose interferenze, si pone subito un’altra domanda. Devo chiedermi quale possa essere e come quantizzare il fattore di distorsione che, inevitabilmente, sarà presente in uscita dai generatori di segnale (forme d’onda). Questa è una domanda sicuramente lecita. E’ una domanda a cui devo dare risposta, poiché al valore di distorsione del generatore di segnale, qualunque esso sia, andrà a sommarsi il valore di distorsione del DST stesso, quando misurerò. Tuttavia discuterò di tutto questo in un contributo successivo, per il momento è meglio restare sui segnali e dispositivi di segnale (DSS).
Due parole sui dispositivi di segnale (DDS) o generatori di forme d’onda e tipi di forme d’onda
Devo ancora spendere due parole sulle forme d’onda che vengono utilizzate durante le fasi di misurazione. I segnali base che posso usare sono sostanzialmente tre: l’onda sinusoidale, l’onda triangolare e l’onda quadra. Tutti questi segnali li posso usare in funzione della tipologia di misura e pertanto, del parametro che voglio determinare. Nella stragrande maggioranza delle misure si usa, comunque sempre, la forma d’onda sinusoidale. Solo a titolo di esempio potrei ricercare con tale segnale: la saturazione, fare misure di potenza d’uscita, di distorsione, tracciare la curva di risposta in frequenza e le curve dei controlli di tono, determinare la sensibilità degli ingressi, il ronzio, il rumore ecc. Con la forma d’onda sia triangolare, sia sinusoidale posso ricercare il sovraccarico d’ingresso e il clipping. Tuttavia soprattutto per la ricerca della distorsione d’incrocio, la forma d’onda triangolare può essere talvolta preferibile. La distorsione d’incrocio si verifica in amplificatori in classe B. Proprio come nel caso del DST in cui, se non erro, lo stadio finale è stato realizzato con tipologia push-pull a simmetria complementare, mediante Darlington figura 22.
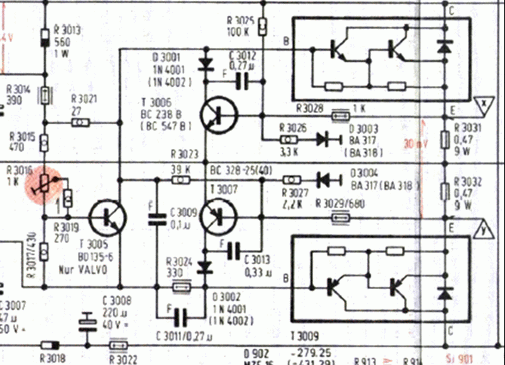
Figura 22 – R20 vista parziale dello stadio finale canale destro.
Figura 22 – R20 vista parziale dello stadio finale canale destro.
Gli amplificatori push-pull funzionanti in classe B presentano, infatti, l’inconveniente della distorsione d’incrocio o crossover, che può essere non del tutto trascurabile qualora non vengano introdotte, in sede di progetto, opportune compensazioni dei circuiti di polarizzazione. In pratica, il segnale in uscita è ricostruito attraverso i contributi combinati dei transistor finali che conducono alternativamente, uno nel semi-periodo positivo, l’altro nel semi-periodo negativo. Qualora le compensazioni sopra descritte non siano presenti, oppure siano mal funzionanti, è possibile osservare, esagerando molto, qualcosa di simile a quanto mostrato nelle figure 23 e 24 con onda sinusoidale o triangolare.

Fig. 23
Fig. 23
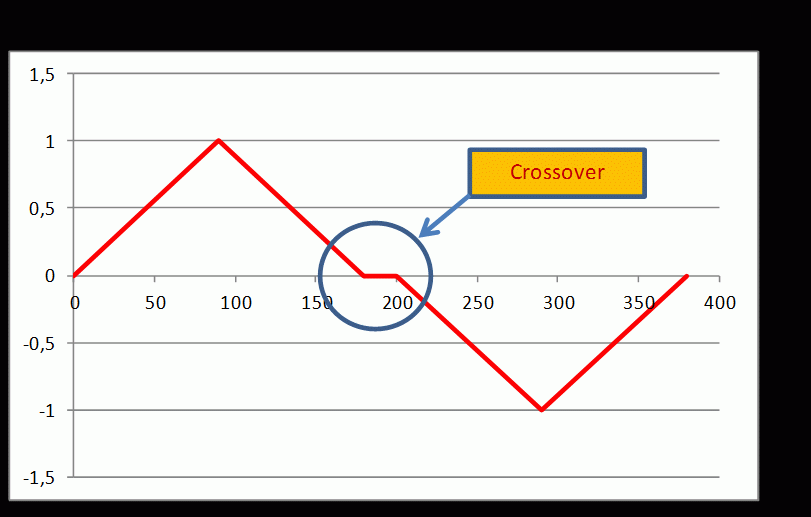
Fig. 24
Fig. 24
Una notazione un po’ particolare merita, infine, la forma d’onda che prende il nome di onda quadra. Un onda quadra, è l’andamento di un segnale che conserva un valore costante di ampiezza in valore assoluto pari a (X) per un determinato periodo (P) passando poi, istantaneamente, a un altro valore di ampiezza in valore assoluto (X1 = X), anch’esso costante e con periodo (P1 =P) al termine del quale, ritorna al primo valore (X) ricominciando il ciclo. Analiticamente l’onda quadra è la risultante della somma di infinite onde sinusoidali, le cui caratteristiche sono determinate dalla serie del Fourier. In altri termini, si tratta di un’onda sinusoidale (Fondamentale) di frequenza e di ampiezza pari a quelle dell’onda quadra, alla quale si sommano via via all’infinito, onde sinusoidali dette armoniche (tutte dispari) di intensità decrescente e di frequenza multipla della fondamentale stessa. Un onda quadra è definita matematicamente dalla seguente:
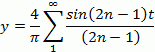
Il cui sviluppo in serie è rappresentabile così:
![]()
Per vedere gli effetti della somma delle armoniche sulla fondamentale, basta aprire un foglio di Excel e implementare un breve calcolo dello sviluppo in serie per una trentina di armoniche, avendo cura di rappresentare graficamente il risultato step by step. Nelle figure successive dalla figura 25 alla figura 30, si vede il risultato di una simile azione. Osservando i vari grafici nel loro progredire, si vede bene come la somma successiva di armoniche sulla sinusoidale fondamentale, finisca per distorcere quest’ultima, fino a portarla ad assumere la forma definitiva di onda quadra perfetta, quando si raggiunge la sommatoria di circa 100 armoniche. Nel mio esempio, tuttavia, mi sono fermato alla 29 armonica, perché è più che sufficiente per evidenziare la trasformazione progressiva della sinusoidale in quadra.
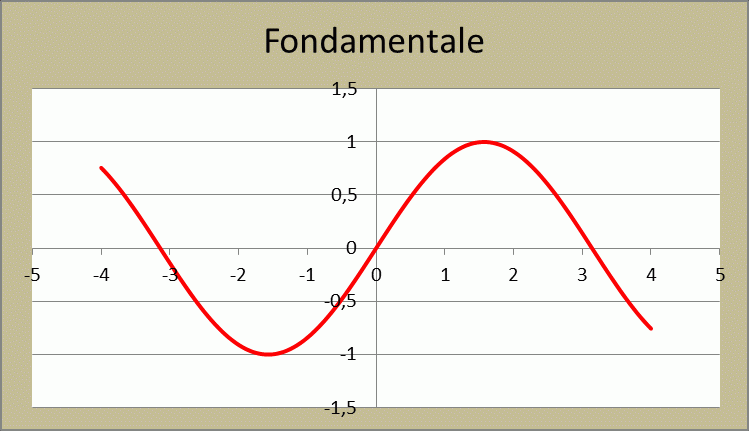
Figura 25 – Sinusoidale fondamentale
Figura 25 – Sinusoidale fondamentale
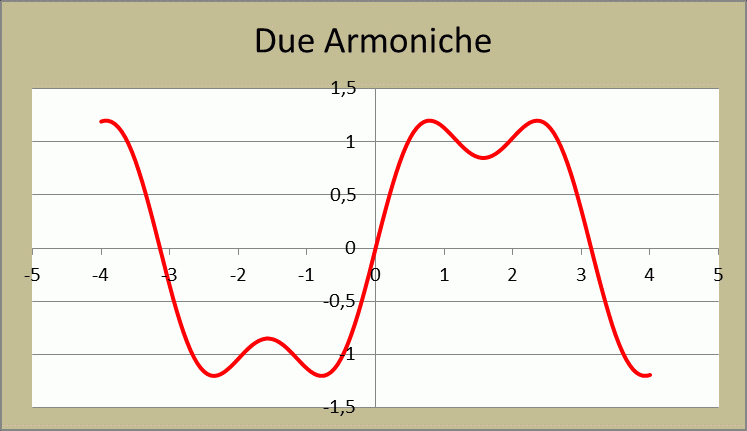
Figura 26 – Due armoniche
Figura 26 – Due armoniche

Figura 27 – Tre armoniche
Figura 27 – Tre armoniche
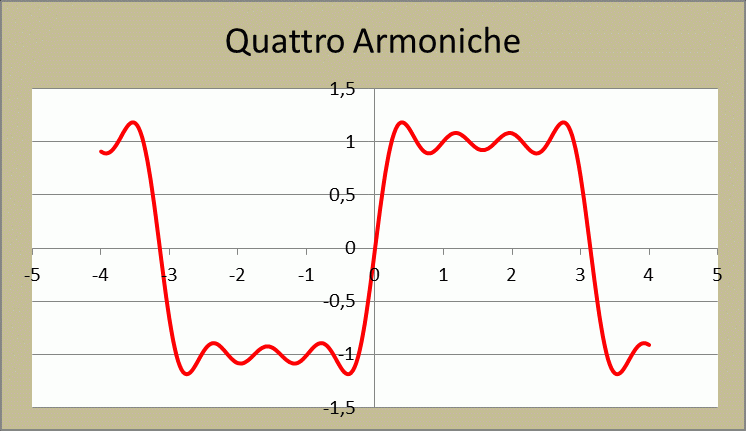
Figura 28 – Quattro armoniche
Figura 28 – Quattro armoniche
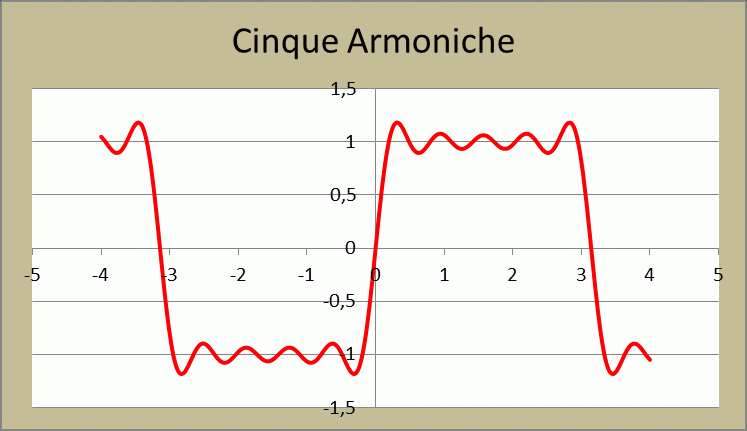
Figura 29 – Cinque armoniche
Figura 29 – Cinque armoniche
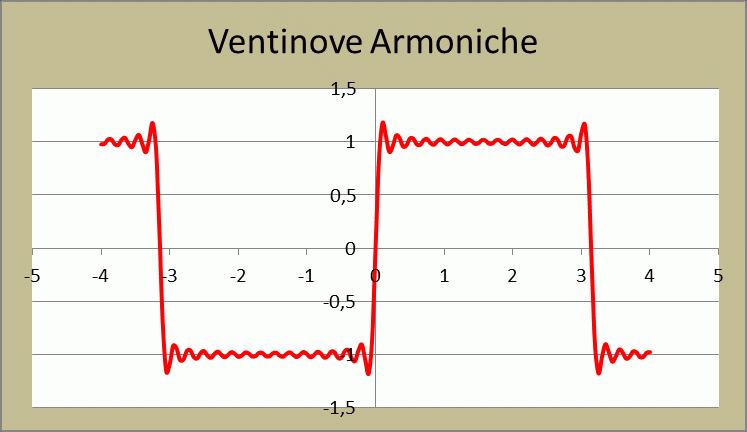
Figura 30 – Ventinove armoniche
Figura 30 – Ventinove armoniche
Esaminando le immagini precedenti si vede come il tratto orizzontale di massima ampiezza sia positiva sia negativa della forma d’onda, vada configurandosi sempre meglio al crescere delle armoniche, quindi anche al crescere della complessità del segnale. Un onda quadra, infatti, per il suo elevato contenuto di armoniche, è il segnale che maggiormente si avvicina a quello musicale. L’osservazione del tratto orizzontale, ci racconta parecchie cose sul dispositivo sotto test.
L’eventuale pendenza o l’inarcatura del tratto orizzontale dell’onda quadra, ci dice come l’amplificatore si comporta sia alle basse, sia alle medie, sia alle alte frequenze.
Inoltre, la possibile inclinazione del tratto orizzontale mostra la tendenza del DST ad attenuare o esaltare alcune bande di frequenza. In particolare, facendo riferimento alle prossime figure 31, 32, 33 e 34, dove sono evidenziati i punti cruciali in cui le deformazioni dell’onda quadra, mostrano le attitudini, o meno, del DST a reagire in modo lineare al segnale, si possono evidenziare i seguenti casi:
- Il DST tende ad attenuare (debolmente o fortemente) le frequenze Basse.
- Il DST tende a esaltare (debolmente o fortemente) le frequenze Basse.
- Il DST tende ad attenuare (debolmente o fortemente) le frequenze Alte.
- Il DST tende a esaltare (debolmente o fortemente) le frequenze Alte.
- Il DST attenua (debolmente o fortemente le frequenze Medie.
- Il DST esalta (debolmente o fortemente) le frequenze Medie.
- Il DST tende ad auto-oscillare sulle frequenze Basse.
- Il DST tende ad auto-oscillare sulle frequenze Alte.
- Il DST presenta in modo, più o meno marcato, il fenomeno di phase shift.
Piccolo breviario dell’onda quadra
Le immagini seguenti si riferiscono alle deformazioni del segnale in uscita dal DST. Tali deformazioni, ci raccontano qual è l’interazione prodotta dal DST stesso sul segnale in ingresso, quando i controlli di tono sono in posizione flat. Si tenga presente che le deformazioni della quadra sono disegnate in modo volutamente esagerato, per una miglior comprensione.
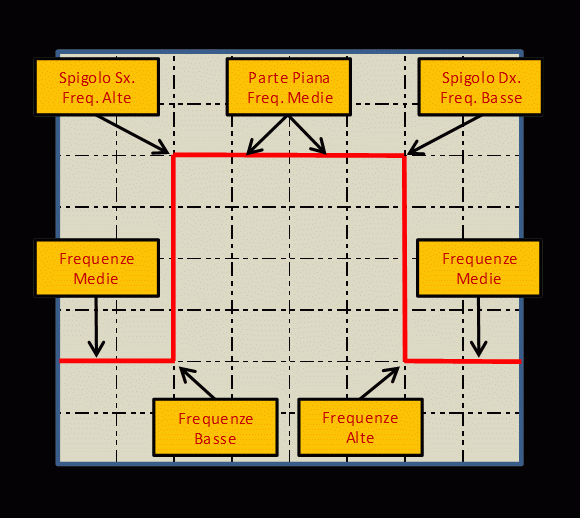
Figura 31 – Regioni significative dell’onda quadra.
Figura 31 – Regioni significative dell’onda quadra.
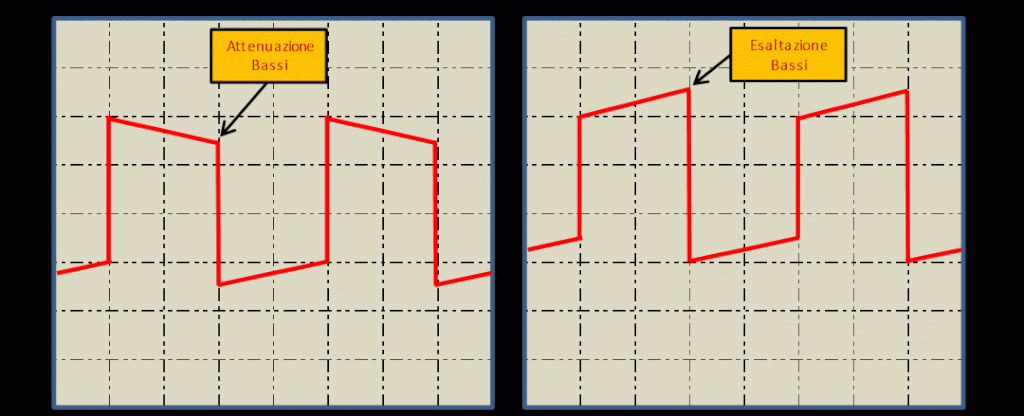
Figura 32 – Onda quadra – Pendenze esaltazione/attenuazione toni bassi
Figura 32 – Onda quadra – Pendenze esaltazione/attenuazione toni bassi
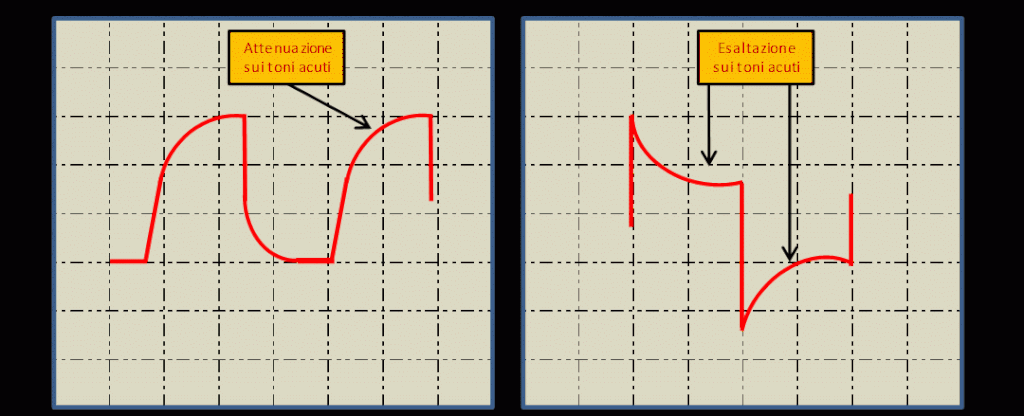
Figura 33 – Onda quadra – Arrotondamenti esaltazione/attenuazione toni acuti
Figura 33 – Onda quadra – Arrotondamenti esaltazione/attenuazione toni acuti
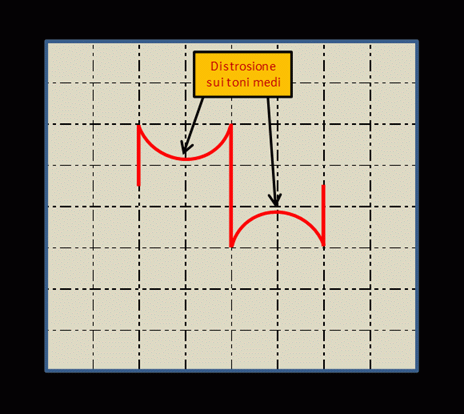
Fig. 34 – Presenza di distorsione in gamma media
Fig. 34 – Presenza di distorsione in gamma media
Le figure 31, 32,33 e 34 mostrano zone ed alcuni effetti significativi, a cui si deve prestare attenzione esaminando il segnale di uscita dal DST. Quando il DST amplifica in modo lineare, si osservano tratti veramente orizzontali dell’onda quadra. Al contrario ove ci sia un’attenuazione, ad esempio delle frequenze basse, i tratti orizzontali saranno inclinati verso il basso a partire dallo spigolo destro. In caso, invece, di esaltazione delle frequenze basse, vedremo che i tratti saranno inclinati verso l’alto, sempre a partire dallo spigolo Dx. figura 33. L’azione del DST sulle frequenze alte, sarà invece visibile come arrotondamento dello spigolo Sx. dell’onda quadra figura 34, che sarà rivolto verso il basso se gli alti sono attenuati, o rivolto verso l’alto se c’è esaltazione delle frequenze alte. Procedendo in modo del tutto simile, si potrà esaminare l’intervento e gli effetti dei controlli di tono e dei vari filtri disponibili sul DST. Naturalmente l’estensione alla gamma di frequenze alte riprodotte o gestibili dal DST, sarà tanto maggiore, quanto più l’arrotondamento dello spigolo Sx. si avvicinerà alla forma dell’angolo retto. Per la risposta ai transitori bisognerà, invece, fare attenzione alle sovra-oscillazioni, qualora si presentino e al tempo di salita che dovrà, ovviamente, essere il più breve possibile. Se è breve, si ha massima prontezza di risposta da parte del DST.
Perché usare l’onda quadra?
Perché utilizzando l’onda quadra sono sufficienti un numero davvero ristretto di prove a pochi range di frequenza. Tanto che, con poche prove, si può capire quale sia l’andamento complessivo in frequenza del DST. Possiamo asserire questo, sulla base dell’analisi armonica. Sappiamo come già visto che, per mezzo dell’analisi di Fourier (analisi armonica o analisi nel dominio della frequenza), un segnale sinusoidale può essere scomposto nella somma di una sinusoide fondamentale, più tutta una serie di componenti dette armoniche. Abbiamo anche visto che un onda quadra e la risultante della somma d’infinite sinusoidi, tra fondamentale e armoniche dispari.
Sappiamo anche che, più alto è il numero di armoniche prese in considerazione nello sviluppo in serie, più sarà ben definita l’onda quadra risultante. Nella prossima in figura 35, si vede la ripresa del calcolo dello sviluppo in serie dell’onda quadra fatto prima, dove mi sono spinto a prendere in considerazione 91 armoniche.
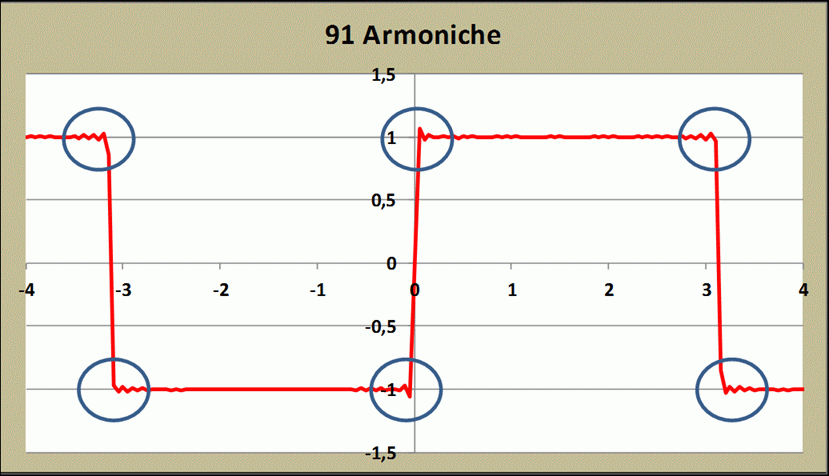
Figura 35 – Ricalcolo sviluppo in serie Onda quadra con 91 armoniche
Figura 35 – Ricalcolo sviluppo in serie Onda quadra con 91 armoniche
Come si vede, rispetto alla precedente figura 30, più si aumenta il numero di armoniche e maggiormente appaiono ben definiti la parte orizzontale e gli spigoli dell’onda quadra. Tra le altre cose, non appena si supera il centinaio di armoniche, anche le piccole imprecisioni ancora presenti ed evidenziate nei cerchi tendono a sparire completamente, lasciando sul grafico solo una ben definita onda quadra. Questo, però, vuol anche dire che, se la fondamentale ha frequenza pari a 1kHz la sua centesima armonica avrà frequenza pari a 100kHz. Dunque, se tanto mi da tanto, quando inietto nel DST, un onda quadra di frequenza 1kHz e la vedo restituita, in forma del tutto perfetta, posso essere certo che il mio DST lavorerà correttamente, anche con le armoniche che si trovano ben oltre la banda audio (20Hz ÷ 20kHz). Tanto che potrò predire, con un buon grado di confidenza, un corretto funzionamento del DST su una banda passante che si estende ben oltre i 20kHz. Se poi voglio capire, quale sia la vera frequenza di taglio superiore a -3 dB della banda passante, allora basta misurare il tempo di salita dell’onda quadra, cosa che farò, seguendo ciò che si vede nelle figure 36 e 37.
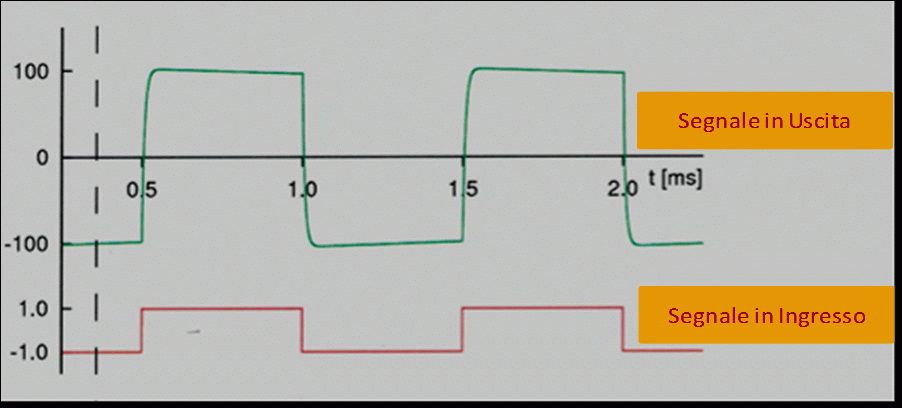
Figura 36 – Deformazione onda quadra in uscita che mostra un ritardo nel tempo di salita
Figura 36 – Deformazione onda quadra in uscita che mostra un ritardo nel tempo di salita
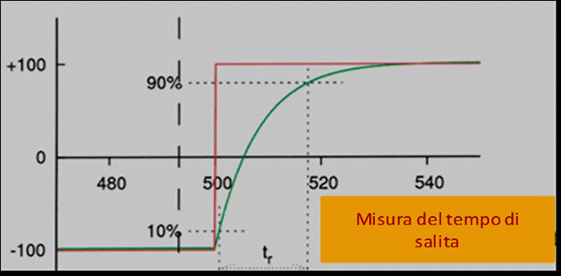
Figura 37 – Misura del tempo di ritardo
Figura 37 – Misura del tempo di ritardo
Ora, per tutti quelli che hanno resistito fin qui a leggere molta teoria, è giunto il momento di passare ai fatti strumentali. Inizierò l’analisi del Receiver Grundig R20, osservando il suo comportamento alla sollecitazione dell’onda quadra, immettendo le seguenti frequenze: 40Hz, 400Hz, 1kHz, 10kHz.
Precauzioni sul segnale di ingresso e sua ampiezza
Se consideriamo il nostro DST come un quadrupolo senza prestare troppa attenzione alla sua costituzione interna, quello che si fa in questi casi è: introdurre un segnale dalle caratteristiche perfettamente conosciute nel DST, osservando e comparando costantemente il segnale in uscita con quello in ingresso. Tutto ciò è fatto per stabilire quali siano le eventuali alterazioni sul segnale apportate, o no, dal DST stesso. In definitiva, osserverò come il DST Grundig Receiver R20, reagisce alla sollecitazione di un segnale a onda quadra variabile in frequenza. Come prima cosa dovrò selezionare un ingresso, tra quelli disponibili. Faccio questo, in modo da poter applicare un segnale avente una caratteristica di ampiezza tale da non saturare l’ingresso stesso. Inizierò classicamente con un segnale a 1kHz, per vedere come il DST lo restituisce rispetto a quello in ingresso. Poi eseguirò un passaggio a tutte le altre frequenze previste, cioè: 40Hz, 400Hz e 10kHz. Infine mi fermerò alla misurazione del tempo di salita e all’illustrazione qualitativa, dell’azione ed intervento dei controlli di tono, lasciando tutte le altre misure a un secondo successivo contributo.
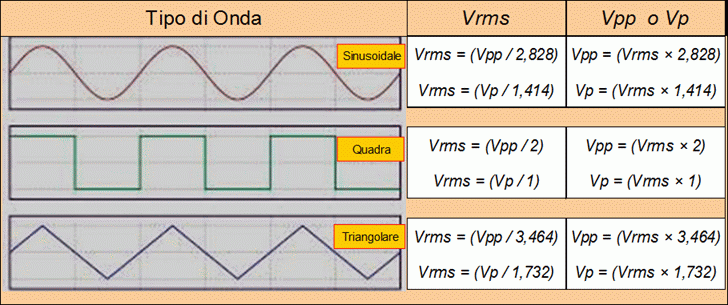
Figura 38 – Trasformazioni tra Volt rms, Volt picco-picco e Volt picco.
Figura 38 – Trasformazioni tra Volt rms, Volt picco-picco e Volt picco.
Se devo iniettare un segnale ac in un’apparecchiatura provvista di numerosi ingressi, alcuni perfino specifici e/o dedicati, la cosa migliore da fare è prendere visione di tutte le sensibilità di ingresso, selezionando quella o quelle che offrono una finestra che non sia strettissima. Una volta scelto l’ingresso sulla base della sua sensibilità devo, ovviamente, adattare il segnale uscente dal generatore, che è sempre espresso in Volt picco-picco, alla sensibilità rms dell’ingresso scelto.
In questo caso, avendo scelto l’ingresso TB2 ovvero [170mV su 470kOhm] imposterò, seguendo le indicazioni della figura 38, l’uscita del generatore per un’ampiezza picco-picco dell’onda quadra pari a 280mV. Il che significa avere in ingresso un segnale pari a 140mV rms, ben al disotto dei 170mV previsti per l’ingresso TB2. In questo modo potrò effettuare tranquillamente le misure senza saturare l’ingresso stesso.
Comportamento del DST Grundig Receiver R20 all’onda quadra.
Cosa mi aspetto di osservare alle frequenze scelte
Se tutto va come dovrebbe andare, mi aspetto di osservare quanto descritto per un buon amplificatore hifi, da Gordon J. King nel suo libro intitolato: “The Audio Handbook”; che sostanzialmente è quanto segue:
- Con i controlli tono in flat, alla frequenza di 1kHz devo osservare un onda quadra restituita in modo perfetto e priva di qualsiasi deformazione. In particolare, i tratti rettilinei devono essere veramente rettilinei con spigoli poco arrotondati e pendenze assolutamente nulle.
- Sempre con i controlli tono in flat, a 10kHz posso osservare un arrotondamento sullo spigolo sinistro della quadra non molto pronunciato che, comunque, non comprometta totalmente il tratto verticale della quadra stessa.
- Sempre con i controlli tono in flat, a 400Hz, la quadra deve presentarsi quasi identica al segnale entrate e si può evidenziare solo una debolissima pendenza del tratto orizzontale, a partire dallo spigolo sinistro verso il destro.
- Sempre con i controlli tono in flat, a 40Hz, è consentita un’inclinazione e anche una debole inarcatura del tratto orizzontale della quadra. Come la frequenza 400Hz, anche qui la pendenza va dallo spigolo sinistro verso il destro.

Figura 39 – Come deve essere la risposta quadra per un buon amplificatore (G.J.King)
Figura 39 – Come deve essere la risposta quadra per un buon amplificatore (G.J.King)
Con riferimento alla figura 39, procedo all’applicazione del segnale ad onda quadra sul DST R20. E’ facile osservare, nelle figure da 40 a 43, come la risposta del receiver, quando sollecitato dall’onda quadra, si comporti sostanzialmente come atteso.
Frequenza di 1kHz.

Figura 40 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 1kHz.
Figura 40 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 1kHz.
Frequenza di 40Hz.
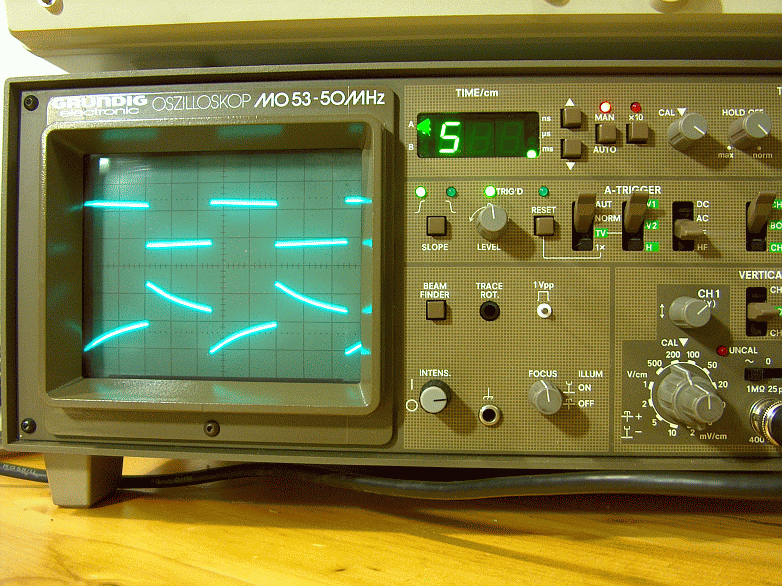
Figura 41 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 40Hz.
Figura 41 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 40Hz.
Frequenza di 400Hz.

Figura 42 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 400Hz.
Figura 42 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 400Hz.
Frequenza di 10kHz.
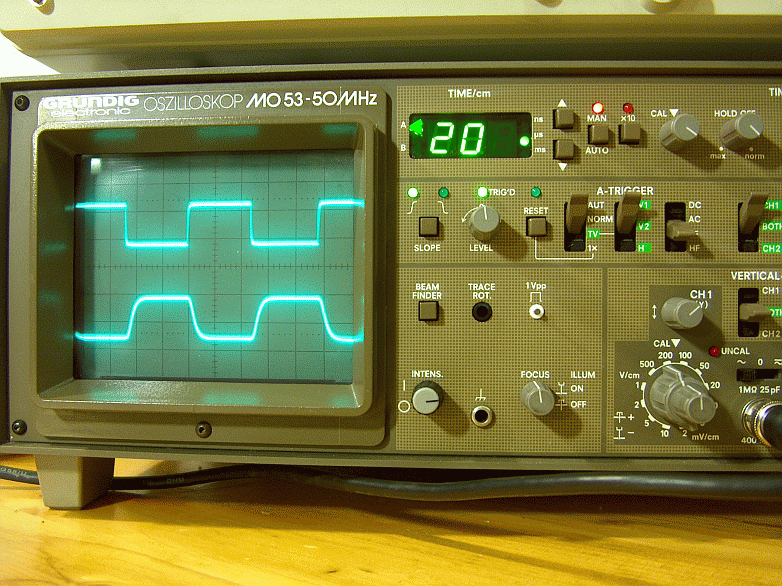
Figura 43 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 10kHz.
Figura 43 – Risposta del DST R20 alla sollecitazione sinusoidale di frequenza 10kHz.
Indagine relativa al tempo di salita dell’impulso quadro.
La disponibilità di componenti elettronici ad alta frequenza di taglio, rende possibile ottenere risposte in frequenza, dei singoli stadi di amplificazione, che si estende ben oltre il range [20Hz÷20kHz] e può arrivare fino al campo delle radiofrequenze. Tutto ciò, però, vuol anche dire che, a un certo punto, il progettista elettronico dovrà imporre dei tagli sulla banda passante per evitare il passaggio di segnali indesiderati. Ci sono diverse scuole di pensiero a riguardo. C’è chi opera tagli intenzionali alle alte e alle basse frequenze, con l’intento di migliorare le prestazioni audio della catena amplificatrice. Alcuni progettisti preferiscono tagliare i bassi sotto i 30Hz, mentre altri propugnano la massima estensione anche alle basse frequenze, per evitare evidenti effetti di differenziazione dell’onda quadra. Si veda per questi effetti di differenziazione la precedente figura 41. Praticamente poi, occorre comunque sempre produrre tagli della banda passante a bassa frequenza per minimizzare rombo e segnali di tipo infrasonico. C’è poi da dire che molti sostengono che non vi sia, praticamente, vera informazione musicale sotto i 30Hz.
Dunque si è visto che dal lato bassa frequenza, la banda passante può evidenziare effetti dovuti a tagli imposti in sede progettuale. Cosa succede, invece, dal lato alte frequenze? Dal lato delle alte frequenze ci aiuta nuovamente l’onda quadra. Come ho anticipato nelle figure 36 e 37, possiamo farci un’idea di quale sia la frequenza a -3dB della banda passante, utilizzando la relazione esistente tra banda passante e tempo di salita dell’impulso quadro. Il tempo di salita è specificato come: il tempo impiegato dalla tensione all’uscita dell’amplificatore, per salire dal 10% al 90% del suo valore finale. La relazione tra la frequenza di taglio della banda passante a -3dB e il tempo di salita dell’impulso quadro è espressa dalla seguente.
![]()
Dove t è il tempo di salita misurato e f-3dB è la frequenta di taglio superiore della banda passante.
Ora passiamo alla misura del tempo di salita per i DST R20 figura 44.
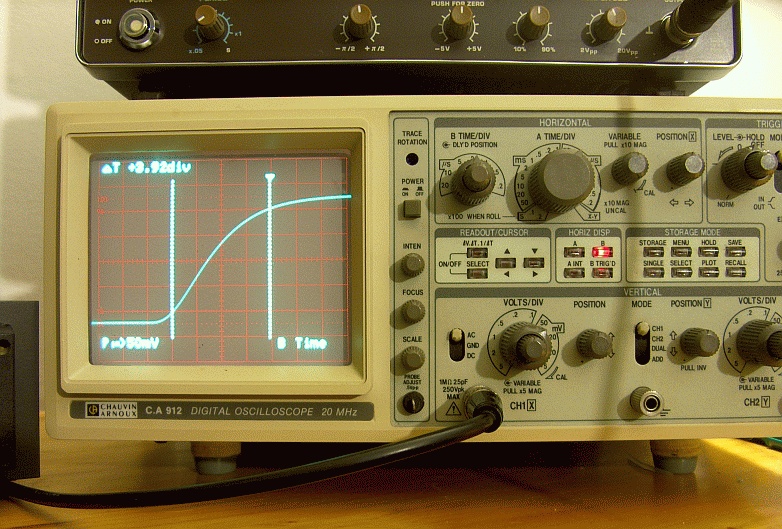
Figura 44 – Misura del tempo di salita del DST R20 = 7,84 ms
Figura 44 – Misura del tempo di salita del DST R20 = 7,84 ms
Commento alla misura del tempo di salita.
Il tempo di salita è risultato pari a 7,84 microsecondi, il che significa una frequenza di taglio a -3dB della banda passante a circa 44600 Hz. più del doppio della banda audio!
Tuttavia le misure fatte con l’oscilloscopio non hanno mai un grado di precisione elevato, così l’ultima parola su questo valore l’avrà il millivoltmetro, quando misurerò la banda passante a -3dB in un prossimo contributo.
Breve panoramica sull’azione e intervento dei filtri Bassi/Acuti sull’onda quadra a 1kHz
Per tutte le immagini che seguono, la traccia superiore mostra sempre il generatore di segnale a 1kHz e la traccia inferiore mostra sempre il DST R20. Aldilà di misure quantitative di guadagno o attenuazione, che comunque eseguirò in un prossimo contributo, le immagini mostrano l’intervento e l’effetto dei controlli di tono del DST R20. Osservando le figure da 45 a 53 è possibile rendersi conto di quale sia l’intervento operato dai controlli di tono sul segnale in ingresso.
In figura 45 la posizione per i controlli di tono è Flat.

Figura 45
Figura 45
In figura 46 il controllo dei bassi attenua 2 posizioni.

Figura 46
Figura 46
In figura 47 il controllo dei bassi attenua 4 posizioni.

Figura 47
Figura 47
In figura 48 il controllo dei bassi esalta 2 posizioni.

Figura 48
Figura 48
In figura 49 il controllo dei bassi esalta 4 posizioni.

Figura 49
Figura 49
In figura 50 il controllo degli acuti attenua 2 posizioni.
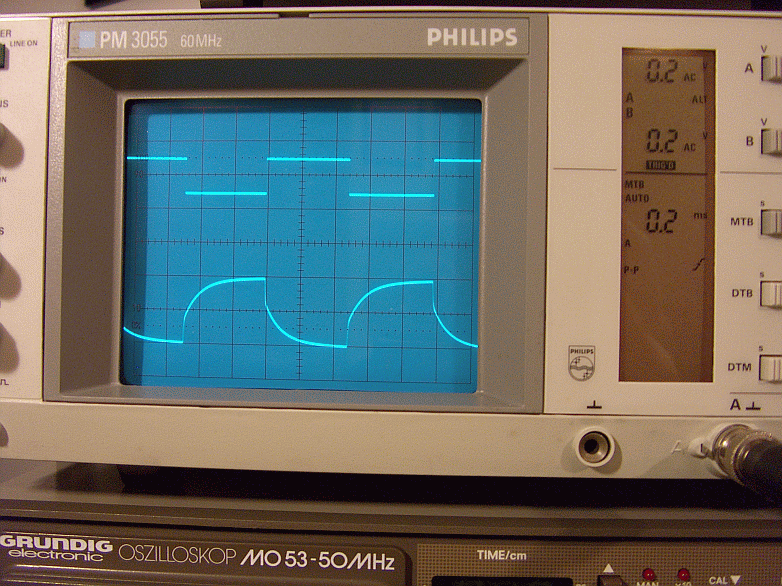
Figura 50
Figura 50
In figura 51 il controllo degli acuti attenua 4 posizioni.
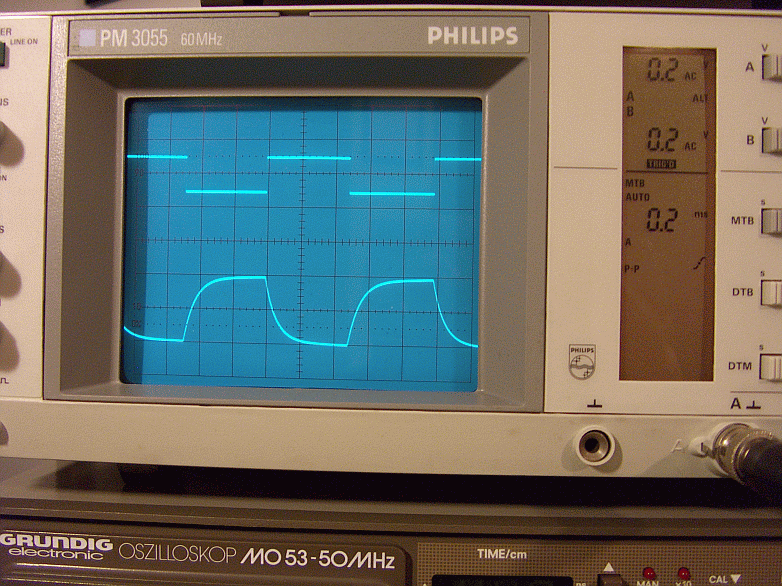
Figura 51
Figura 51
In figura 52 il controllo degli acuti esalta 2 posizioni.

Figura 52
Figura 52
In figura 53 il controllo degli acuti esalta 4 posizioni.

Figura 53
Figura 53
Conclusioni.
In questo contributo ho condotto un’analisi sostanzialmente qualitativa, attraverso il test dell’onda quadra.
Analisi che ha mostrato, anche se non ancora a livello quantitativo, le buone performances del Grundig R20.
Soprattutto per quanto riguarda la larghezza di banda e la sua estensione alle alte frequenze.
Buono è stato pure il tempo di salita, che lascia intravedere una risposta estesa alle alte frequenze, quindi una assai buona larghezza di banda che supera abbondantemente i 40kHz.
In un prossimo contributo provvederò ad un’analisi essenzialmente quantitativa, determinando.
- Risposta in frequenza in forma tabellare e grafica su scala logaritmica.
- Potenza R.M.S. , musicale e di picco più banda di potenza.
- Risposta dei controlli di tono, sia in forma tabellare, sia su grafico logaritmico.
- Il valore di Clipping e sovraccarico d’ingresso.
- Visualizzazione su oscilloscopio della distorsione + rumore residuale.
- Risposta in fase in forma tabellare e grafica.





Però… niente male! Complimenti, hai dimostrato una certa dimestichezza con strumenti di misura che non sono proprio alla portata di tutti.
Nel mio piccolo, posso dire due cose:
1) Pur essendo, la tua, un’iniziativa a scopo puramente divulgativo (e di questo dobbiamo ringraziarti), ritengo che sarebbe stato il caso, prima di sottoporre il nonnetto alle misure, accertare il suo corretto funzionamento (ad esempio, verificando le tensioni di funzionamento, le correnti di riposo, etc.), visto che era fermo da diversi anni. Il fatto che apparentemente funziona non significa anche che funzioni correttamente.
2) Come ti invidio quell’oscilloscopio Grundig!!!
Comunque, grazie ancora e continua!
Ah però, che pezzo (che pezzi)! Grande!
Si, certamente, avrei potuto fare così, ma questo avrebbe comportato l’apertura dell’apparecchio!
Disponendo invece di strumentazione, ho preferito seguire una via, diciamo induttiva. Quello che ho immediatamente fatto, dopo aver comunque sentito l’apparecchio suonare molto bene, è stato quanto segue:
1. Ho considerato l’apparecchio come un quadrupolo scatola nera senza preoccuparmi di come fosse costituito internamente e di tutto ciò che riguardava la sua topologia circuitale.
2. Ho acceso ed atteso che l’apparecchio fosse in temperatura.
3. Ho scelto un ingresso, verificando la sensibilità MASSIMA dichiarata dal costruttore. In questo caso TB = 175mV su 470kOhm. Ho predisposto il generatore per iniettare un segnale sinusoidale di ampiezza picco-picco pari a 175mV R.M.S, cioè un segnale con ampiezza, sempre picco-picco, pari 494.9 mV.
4. Mi sono cioè portato, con il generatore, alla massima ampiezza consentita per l’ingresso selezionato, quindi vicinissimo alle condizioni critiche per l’ingresso stesso.
5. Ho predisposto tutto questo nella certezza che, sicuramente, i progettisti Grundig dovevano aver dimensionato la stabilizzazione delle polarizzazioni e quindi dei punti di lavoro nei vari stadi di passaggio del segnale, in modo da poter soddisfare un evento che trasportasse, attraverso la catena di amplificazione, un segnale di massima ampiezza, restituendolo ancora in modo pulito e corretto.
6. Ho collegato in uscita il carico fittizio (su un canale alla volta).
7. Ho collegato un oscilloscopio al carico fittizio con un canale ricevente il segnale sinusoidale in ingresso e un secondo canale ricevente il segnale in uscita sul carico.
8. A questo punto ho portato il volume dell’apparecchio al massimo. Quindi l’apparecchio stesso alle sue massime prestazioni. In queste condizioni limite ho osservato che, sul segnale in uscita, non fosse presente alcun tipo di clipping e/o dissimmetrie varie.
9. Poiché, appunto, ho osservato un segnale sinusoidale di massima ampiezza restituito in modo pulito alla massima potenza di uscita, per induzione, ho concluso che, evidentemente, i punti di lavoro nella topologia circuitale dovevano essere stabili e centrati, quindi anche le polarizzazioni dovevano lavorare a dovere. Diversamente in quelle condizioni, molto probabilmente, avrei osservato qualche difficoltà nella restituzione di un segnale pulito o debole inizio di dissimmetria monolaterale o bilaterale, magari con inizio di clipping simmetrico o non simmetrico.
10. Inoltre, non osservando presenza di crossover ho concluso che, evidentemente, anche la circuiteria di polarizzazione degli stadi finali in push-pull doveva funzionare in modo corretto.
11. Successivamente ho aumentato l’ampiezza del generatore per andare fuori specifiche e come atteso, ad un certo punto ho osservato clipping bilaterale, indice comunque che l’apparecchio anche in condizioni critiche si comporta correttamente.
12. L’introduzione poi di un segnale quadro a 1kHz, ha restituito in uscita un segnale praticamente perfetto e questo unitamente ad una breve sweeppata manuale con osservazione della quadra sempre nei limiti di un corretto e buon comportamento in frequenza mi ha convinto, sempre per induzione, che l’apparecchio funzionava a dovere, senza bisogno di aprirlo per controllarlo.
Adesso, detta in modo così dettagliato sembra cosa lunga, ma in effetti è cosa da una manciata di minuti.
Evvai Wapillo!!!! sei armato fino hai denti!!!
Cioè, fammi capire: hai impegnato l’ingresso con un segnale di poco sotto alla saturazione, hai fatto lavorare l’ampli con il volume al massimo e non hai rilevato clipping?????
C’è relazione tra sensibilità d’ingresso, guadagno totale e potenza sul carico. Se ci fai caso, la sensibilità di ingresso è sempre espressa in funzione di una determinata potenza d’uscita. Non fanno eccezione le specifiche Grundig per il sintoamplificatore R20. La Grundig, infatti, dichiarava per l’ingresso TB una sensibilità riferita a 30 Watt di potenza nominale per canale, pari a 175mV R.M.S. Questo significa che l’R20 sarà in grado di erogare 30 Watt per canale, quando al suo ingresso TB sarà presente un segnale con ampiezza pari a 175mV R.M.S. E’ questo è un primo punto da memorizzare.
Secondo punto. Sempre da specifiche Grundig la potenza nominale per l’R20 è dichiarata pari a 2 x 30 Watt ovvero 60 Watt totali.
Terzo punto. Nessun progettista che si rispetti si metterà mai a dichiarare 30 Watt per canale, se quel valore è proprio effettivamente il valore massimo limite della sua apparecchiatura, ma si prenderà un po’ di spazio dichiarando qualcosa in meno di ciò che può davvero venir fuori dalla apparecchiatura che ha progettato. In questo modo, non solo si mette al riparo da imprevisti vari, ma ci fa pure una bella figura, fornendo qualcosa di migliore rispetto al dichiarato. Questione di serietà direi.
Infine c’è la relazione tra Volt R.M.S., Watt R.M.S. e resistenza di carico R (Ohm). Questa relazione mi permette di calcolare la tensione che avrò sul carico a partire dalla potenza dichiarata e dal valore della resistenza di carico, come segue:
Volt R.M.S. = (Watt R.M.S. x R)^0.5
Se applico la precedente al nostro R20, per cui Grundig dichiara 60 Watt totali ottengo:
Volt R.M.S. = (Watt R.M.S. x R)^0.5 = (60 x 4)^0.5 = 15.49 Volt R.M.S. = 43.80 Volt picco-picco.
Cosa ci dice la precedente? Ci dice che, a causa del fattore di amplificazione complessivo, il segnale in ingresso originario di 175 mV R.M.S. o anche 494.9 mV picco-picco, verrà amplificato passo dopo passo attraverso l’R20, fino a portarlo in uscita ad un segnale di ampiezza pari a 15.49 Volt R.M.S. o anche 43.80 Volt picco-picco a livello dello stadio finale.
Naturalmente, per far si che ciò avvenga, dovrò agire sul potenziometro del volume e portarlo al massimo, così il segnale che transita potrà subire il previsto guadagno.
In queste condizioni siamo vicinissimi al clipping, ma non lo raggiungeremo poiché siamo ancora in specifica, il segnale in ingresso è a 175 mV R.M.S. e non maggiore!
Infatti, a fronte dei 43,80 Volt picco-picco generati dalla amplificazione del nostro segnale a massima potenza, l’alimentazione si trova a 49 Volt picco- picco duale ( 24.5 + 24.5 ). In questa condizione, se tutte le polarizzazioni funzionano a dovere, i 43.80 Volt picco-picco si troveranno centrati rispetto al range di 49 Volt picco-picco dell’alimentazione e quindi non devo e non posso osservare clipping! Non lo osserverò, semplicemente perché il segnale picco-picco sui finali alla massima potenza dell’R20, ha un’ampiezza che è solo l’89.3 % dell’alimentazione, quindi non ci può essere tosatura! Se, invece, le polarizzazioni non funzionano a dovere, è possibile che qualche punto di lavoro sulle rette di carico in uno o più stadi di amplificazione si sposti dalla centralità in senso positivo o negativo facendo si che, alla fine, quei 5.2 Volt duali di range (49 – 43.80) che dovrebbero esistere a livello dei finali, vengano assottigliati. In tal caso, potrei osservare clipping non simmetrico. Se invece l’ampiezza in ingresso supera il valore 175 mV R.M.S. non vedrò comunque subito clipping simmetrico, perché i progettisti Grundig, naturalmente, si sono lasciati un po’ di spazio ( quei famosi 5.2 volt duali alla massima potenza ) e occorre superare i 200 mV per vedere saturazione e clipping simmetrico.
Si capisce quindi che, in tali circostanze di prova, avendo un segnale sui finali che alla massima potenza ha un’ampiezza picco-picco che sta solo il 10.7% sotto il valore di alimentazione, si riesce a capire – con un buon grado di confidenza – e senza aprire l’apparecchio per misure, se le polarizzazioni funzionano oppure mostrano dei problemi.
Comunque, tutte queste misure arriveranno con il prossimo contributo.